印度|印度初中数学竞赛题:已知t2=22224444-6666,求t的值

文章图片

文章图片
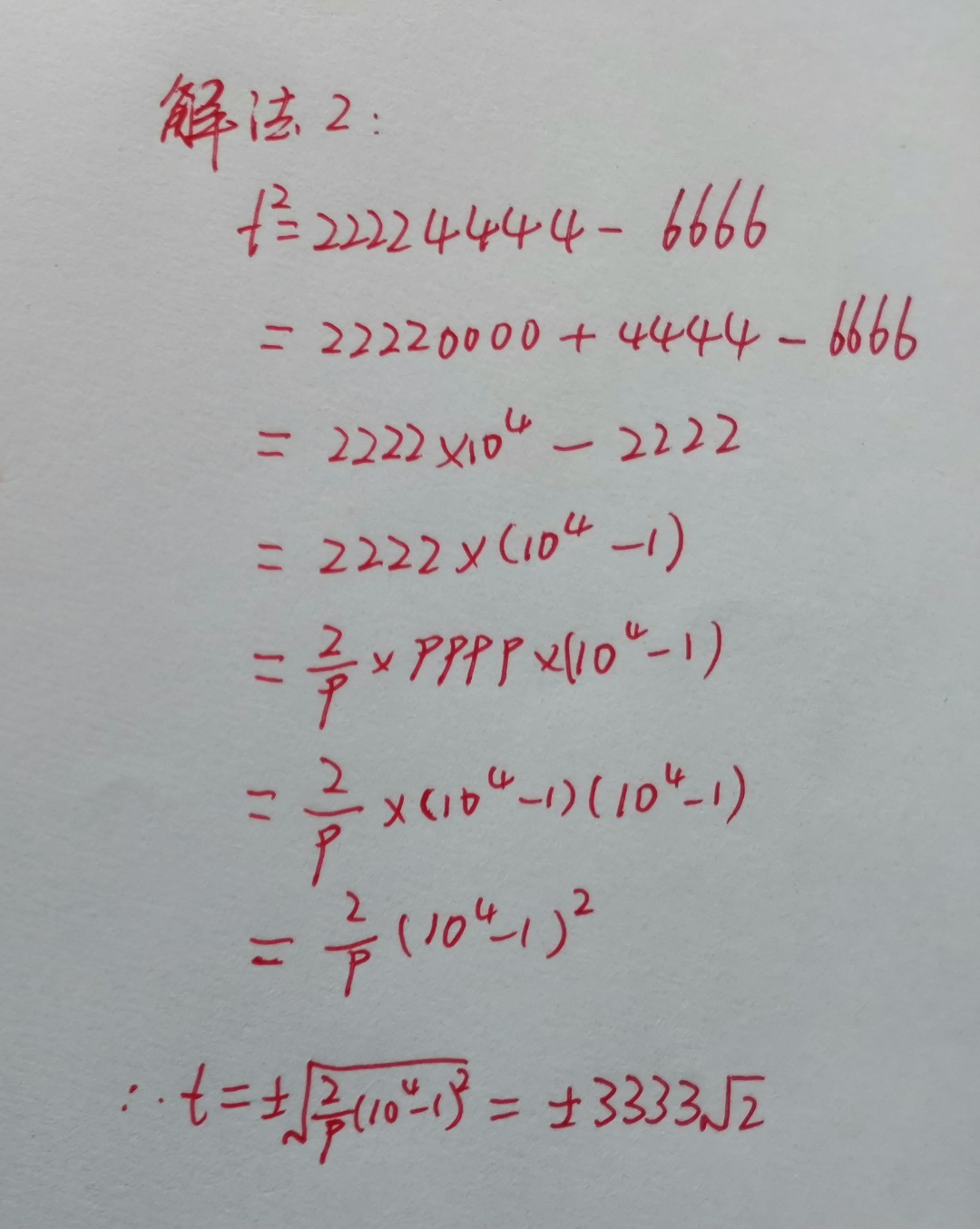
大家好 , 今天和大家分享一道印度初中数学竞赛题:已知t2=22224444-6666 , 求t的值 。 题目数字看起来挺大 , 似乎难度不小 , 但是对于国内很多初中学霸来说 , 这题的难度并不大 , 甚至很多中等成绩的学生都可以做出来 。
本题要求t的值 , 实际上就是一个开平方的题目 。 我们先观察一下题目数字的特点 , 很明显都是数字的重复计算型题目 。 对于这类题目 , 我们一般先想办法化成1111……的形式 , 再化成9999……的形式 。 比如我们先来看一下下面这道题的计算:6666×6666 。
此题如果直接计算 , 肯定是没有问题的 , 但是计算量非常大 , 那么有没有简便计算呢?当然有 。
我们先将其中一个6666进行变形 , 变成6×1111 , 再变成(6×9999)/9=[6×(10^4-1)
/9 , 这个时候再代入原式进行计算即可大大简化计算过程 。 具体过程见下图 。
根据这样这个思路 , 我们可以先把22224444变形成22222222+2222 , 此时整个式子就可以变成22222222+2222-6666=22222222-4444=(2×99999999)/9-(4×9999)/9=[2×(10^8-1)
/9-[4×(10^4-1)
/9 。 这样处理后也就变成了10^n的形式 , 然后再开方即可得到t的值 。
除了这个方法 , 还有没有其他方法呢?当然有 。
我们先来看1111这个数字的另外一种常用处理方法:1111=1×10^3+1×10^2+1×10+1=11×10^2+11等 。 那么 , 题目中的22224444就可以变形成2222×10^4+4444 。 如此一来 , 整个式子就可以变成2222×10^4-2222=2222(10^4-1) , 然后再将2222按照解法一的方法进行处理即可将式子化简 , 最后开方即可得到t的值 。
这一道印度初中数学竞赛题 , 看似难度很大 , 但是方法其实并不难 , 不少老师都讲过这种重复数字的计算技巧 , 所以我找了几个初中学霸做了一下 , 他们都感觉并不太难 。 另外 , 这题还有一个易错点 , 那就是t的值算出来是正负两个值 , 一些同学容易忽略这个负值 。 【印度|印度初中数学竞赛题:已知t2=22224444-6666,求t的值】你觉得这道题难吗?
推荐阅读
- 数学|你见过最讽刺的事是什么?信心满满把试卷给我抄成倒数第二!
- 数学|事业单位又涨工资?除了它,这行也成“香饽饽”,工资不输公务员
- 数学|我们一个被“嫌弃”了23年的数学天才,累死才知道他的价值
- 四川省|四川德阳:某乡镇初中开学,家长几乎自带床板,学校用品额外收钱
- 钱钟书|他高考数学仅有15分,校长复查试卷后十分激动,道:就他了
- 早恋|初中时,这4类女生很受男生喜欢,更容易“早恋”,老师:拦不住
- 考试|初中化学知识框架图,帮孩子贴墙上记,保管考试次次拿满分!
- 数学|我国“最难考”的10所理工大学,录取分超600分,学霸:不在话下
- 数学|数学题:一个四位数与它的各个位上的数之和是1972,求这个四位数
- 中小学|初中时同学家里几个亿,班里的班费被偷了,老师们冤枉他偷班费!


















